[ML] 경사하강법

선형회귀

선형회귀 : 이루어진 데이터들 속에서 결곽값을 잘 내는 모델을 찾는 것
- 경사하강법
- sklearn 라이브러리
- 회귀분석 방법도 있다. 링크

우리가 알아볼 것은 경사하강법이다!</br>

경사하강법으로 선형회귀 계수 구하기

선형회귀의 목적식 : ${\parallel y - X_\beta \parallel}_2$ (= $L_2$-norm)
선형회귀의 목적식을 최소화 하는 $\beta$를 찾는것이 목적!

다음과 같은 Gradient 벡터를 구해보자.

목적식

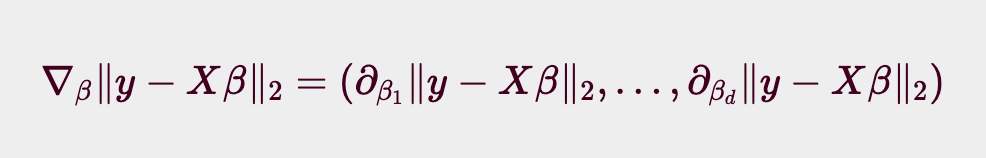
이 때 $\beta$ 의 k번째 계수에 해당하는 $\beta_k$를 가지고 목적식을 편미분하는 식을 풀어서 보면 아래와 같은 식이 된다.

목적식2

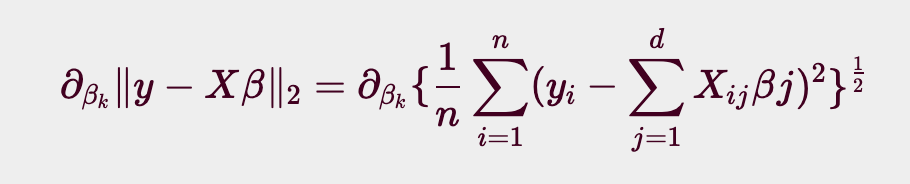
여기서 조심할 점은, 일반적인 수학의 $L_2$ - norm 과 풀이 방식이 살짝 다르다는 것.

여기서 사용하는 $L_2 - norm$은 모델 학습에 사용되는 것이므로, n개의 데이터셋을 가지고 있다는 가정하에 출발한다. 따라서 단순히 $\sum_{i=1}^{n}$에 $\surd$을 바로 씌우는 것이 아닌, $1/n$ 로 형균을 내준 뒤에 씌어준다.

이 때에 사용되는 Loss는 RMSE (Root Mean Squared Error) 이다. 다음과 같은 도출과정을 따른다.

벡터의 거리는 $L_2-norm$ 으로 계산한다.
SE(Sqaured Error) 는 각 데이터별로 정답과 예측 벡터의 차이를 $L_2-norm$ 제곱으로 계산한다.
MSE (Mean Squared Error) 는 SE 를 데이터의 숫자만큼 나누어준다.(평균내기)
RMSE (Root Mean Squared Error) 는 MSE 에 제곱근을 취해준다.

이를 계산하여 정리하면 다음과 같다.

목적식3

따라서 이제, 목적식을 최소화하는 $\beta$ 를 구하는 경사하강법 알고리즘을 다음과 같이 표현할 수 있다.

목적식4

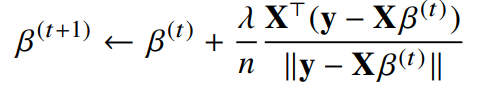
t를 반복적으로 계산하다 보면 목적식을 최소화하는 $\beta$ 를 구할 수 있음
이전과정에 비해, 다변수인 것을 제외히ㅏ면 모든 요소가 같음
$\beta^{(t)}$ : t번째 단계에서의 coefficient
$\lambda$ : 학습률 - 수렴속도 지정
$\nabla_{\beta}$ : gradient vector
$\lambda \nabla_{\beta} \parallel y-x\beta (t) \parallel$ : gradient factor

선형회귀의 목적식은 L2-norm 과 같고, 경사하강법에서 L2-norm 대신 L2-norm의 제곱을 사용하는 것도 가능하다. 둘은 동일한 결과를 가져온다.

목적식5

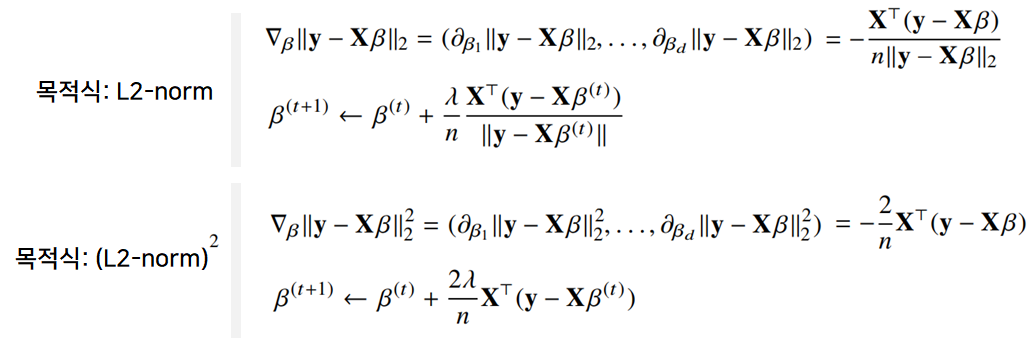
경사하강법 기반 선형회귀 알고리즘

  
# Input: X, y, lr, T
# Output: beta
"""
norm: L2-norm을 계산하는 함수
lr: 학습률
T: 학습횟수
"""
for t in range(T):        # eps로 사용가능, 지정된 시간의 종료조건
    error = y - X @ beta
    grad = - transpose(X) @ error # @: 행렬곱
    beta = beta - lr * grad

위와 같은 경사하강법 알고리즘을 이용해, 무어-팬로즈 역행렬을 사용하지 않고도 계수 $\beta$ 를 찾을 수 있다.

  
# numpy를 활용한 경사하강법 수행 예시
import numpy as np
X = np.array([[1,1],[1,2],[2,2],[2,3]])
y = np.dot(X, np.array([1,2])) + 3
beta_gd = [10.1, 15.1, -6.5] # [1,2,3]이 정답 - 지금 값은 무작위 값
# intercept항 추가
# y 절편을 추가하면, y = ax + b의 b가 bias term의 역할을 해서 계산이 용이하다.
X_ = np.array([np.append(x,[1]) for x in X])
for t in range(5000):
    error = y - X_ @ beta_gd
    # error = error / np.linalg.norm(error)
    grad = - np.transpose(X_) @ error
    beta_gd = beta_gd - 0.01 * grad
print(beta_gd)
# [1.00000367 1.99999949 2.99999516]

lr 은 학습률에 관한것으로 실제로 학습에 지대한 영향을 끼친다. 학습률이 낮을 시 학습속도가 느려지며, 학습률이 크다면 불안정한 gredient 움직임이 발생한다.

경사하강법이 수렴하지 않을 때 - 확률적 경사하강법

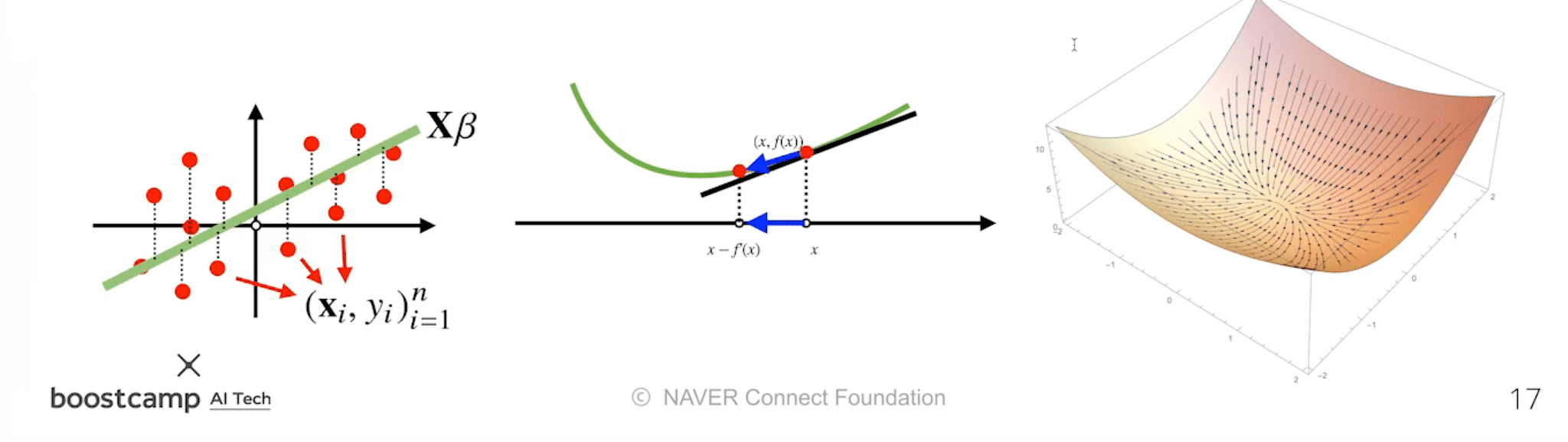
경사하강법사진1

이론적으로, 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해서는, 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어있다.

특히, 선형회귀 목적식 ${\parallel y - X\beta \parallel}_2$ 는 회귀계수 $\beta$ 에 대해 볼록함수 이므로, 알고리즘을 충분히 돌렸을 경우 수렴이 보장된다.

그러나, 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로, 수렴이 항상 보장되지는 않는다.

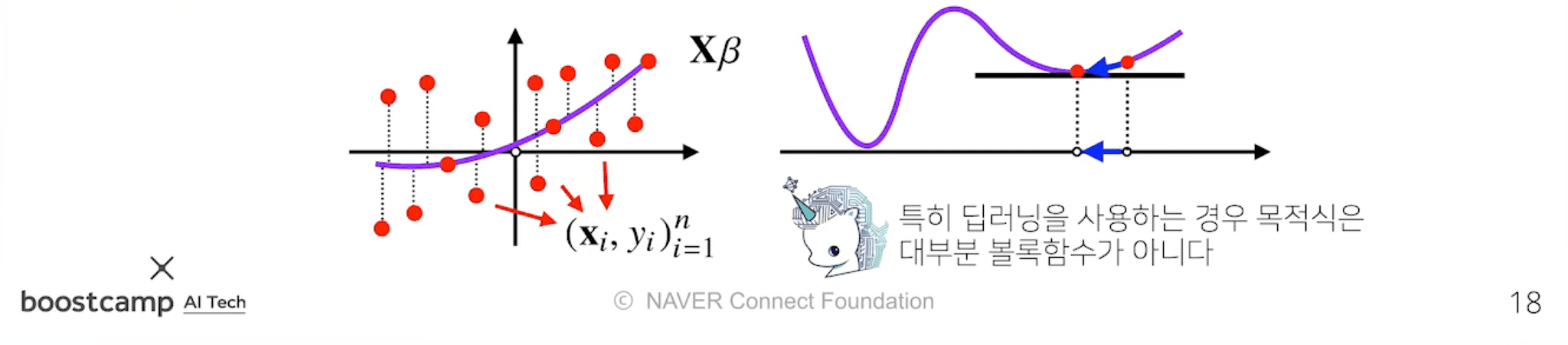
경사하강법사진2

특히 딥러닝을 사용하는 경우는 목적식이 대부분 볼록함수가 아니므로,

이 경우 일반적인 경사하강법이 아닌 확률적 경사하강법(SGD) 을 사용한다.

확률적 경사하강법은 모든 데이터를 사용해서 업데이트 하는 대신에, 데이터 하나 또는 일부를 활용하여 업데이트 하는 방식이다.

확률적 경사하강법의 원리 : 미니배치 연산

경사하강법 (GD) 는 전체 데이터를 이용하여 목적식을 계산한다.

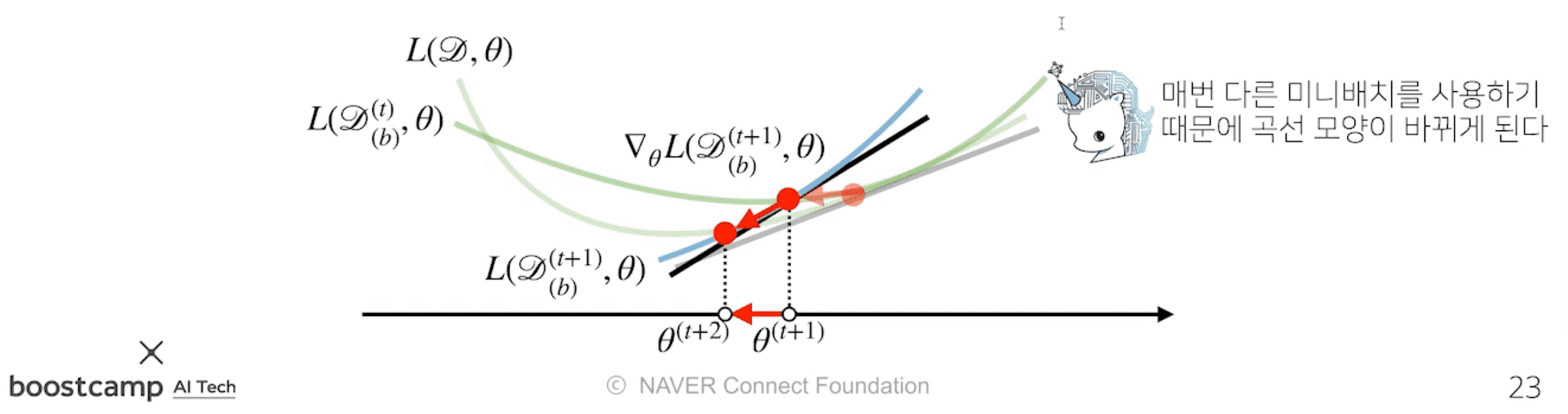
경사하강법3

반면 SGD는 미니배치를 가지고 계산한다. 따라서 매 step 마다 다른 미니배치를 사용할 때마다 목적식의 모양이 점점 바뀌게 된다.

즉, Local MiniMum (극소점) 을 탈출할 수 있다는 말!

하지만 간과하지 말아야 할 것이 있다.

극소점을 탈출할 수 있다는 말은 global minimum을 탈출할 수도 있다는 말이다.

이는 SGD의 단점 중 하나로, global minimum 근처까지는 빠르게 수렴하지만 정작 정확한 global minimum 극소값에는 도달하지 못하고 진동하는 경우가 많다.
반면, GD 는 연산량과 시간이 많이 필요하지만 전체 배치를 통해 모든 점에서 일정한 목적식을 활용하여 global minimum 으로 확실히 수렴 가능하다.
이와 같은 SGD의 문제점은 lr 을 점점 줄여나가는 방식으로 step size 를 줄임으로써 어느정도 해결할 수 있다.

SGD는 볼록이 아닌 목적식에서도 사용 가능하므로 경사하강법보다 머신러닝 학습에 더 효율적이다.

다만, 경사하강법처럼 정확하게 gradient 벡터를 계산해서 흐르는것이 아니므로, 이동방향이 좀 튀는 경향 이 있다.
그렇지만, 결국 데이터를 가지고 gradient 벡터를 계산해서 움직이기 때문에 최솟점으로 향한다는 것은 같다.
또한, 미니배치를 가지고 연산하므로, 각각의 gradient 벡터 계산에 있어서 연산속도가 훨씬 빠르다.

단, SGD에서는 기존의 경사하강법에서 고려했던 학습률(learning rate), 학습횟수(T)에 더해 미니배치 사이즈까지 고려하여 학습해야한다.

참고한 자료 :

https://blogik.netlify.app/BoostCamp/U_stage/05_gradient_descent/

[ML] 경사하강법

선형회귀

경사하강법으로 선형회귀 계수 구하기

경사하강법 기반 선형회귀 알고리즘

경사하강법이 수렴하지 않을 때 - 확률적 경사하강법

확률적 경사하강법의 원리 : 미니배치 연산

Further Reading

[ML] 선형모델과 역전파

[ML] Math_AI 확률론

[ML] Modern CNN