전파모형과 전파 최대화
목표
- 그래프를 통한 정보의 전파에 대해 나타낼 수 있음
- 수학적 모형화를 통한 전파 과정에 대해 설명
- 두가지 전파 모형이 존재
- 의사결정 기반
- 확률적 전파기반
의사결정 기반의 전파모형
- 언제 의사결정 기반의 전파모형을 사용할까? 라인 vs 카카오톡
- 의사결정 기반의 전파 모형의 대표적 예시, 선형 임계치 모형
전파모형이 필요한 이유
- 주변 사람들의 의사결정이 본인의 의사결정에 영향을 미친다.
- 주변 사람들의 의사결정을 고려하여 각자 의사결정을 내리는 경우에 의사결정 기반의 전파 모형을 사용한다.
선형 임계치 모형(Linear Threshold Model)
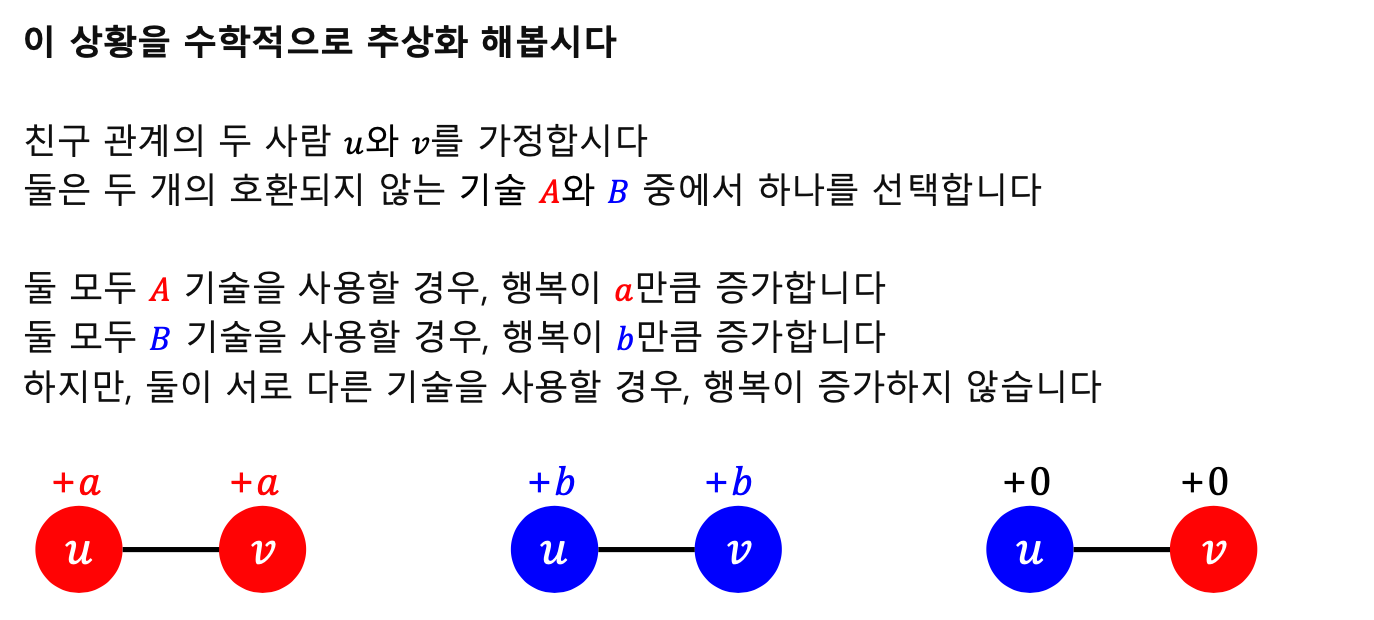
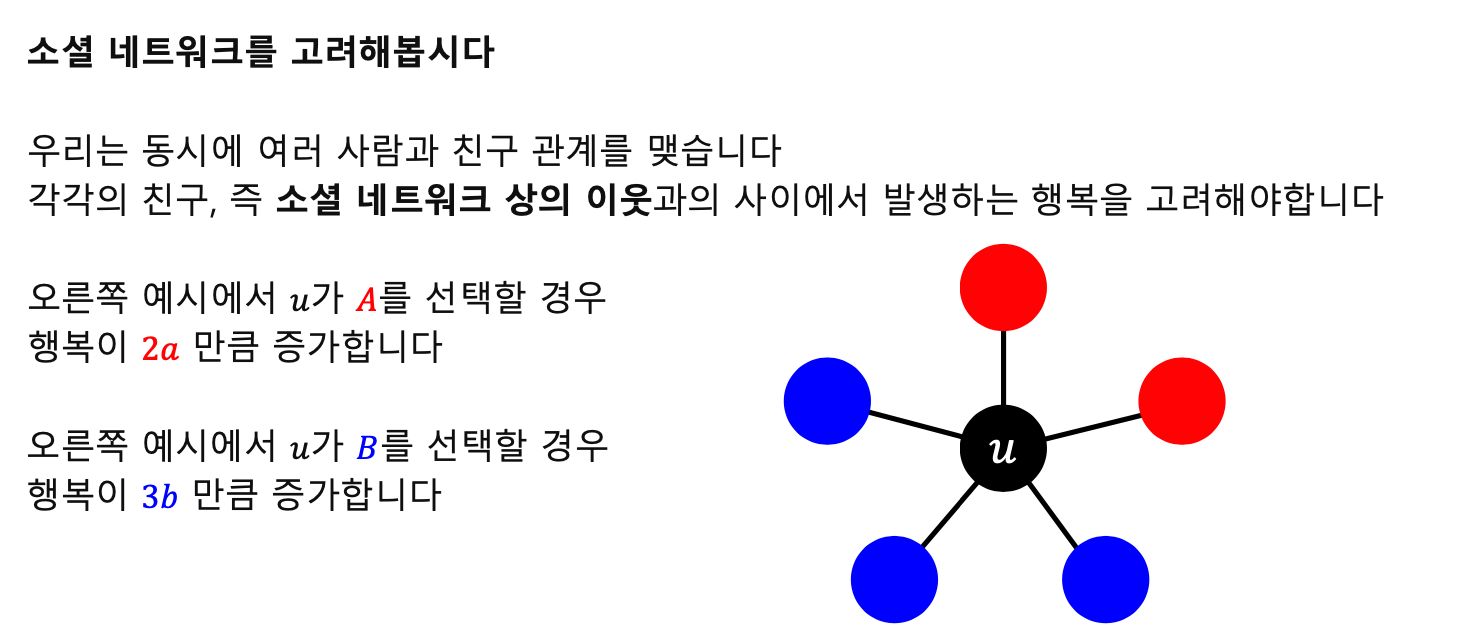
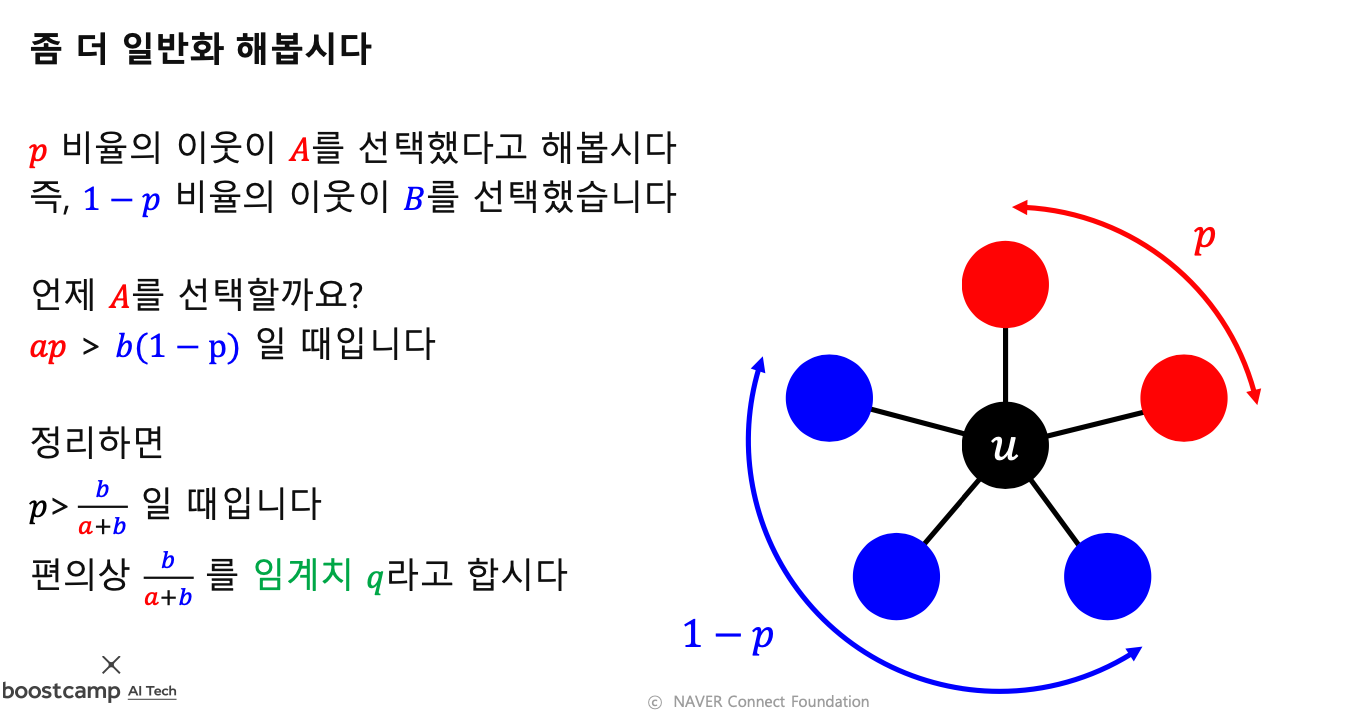
- $p$ 는 A를 선택할 확률
- $p > q$ 일때, A를 선택
- 각 정점은 이웃 중 𝐴를 선택한 비율이 임계치 𝑞를 넘을 때만 𝐴를 선택한다.
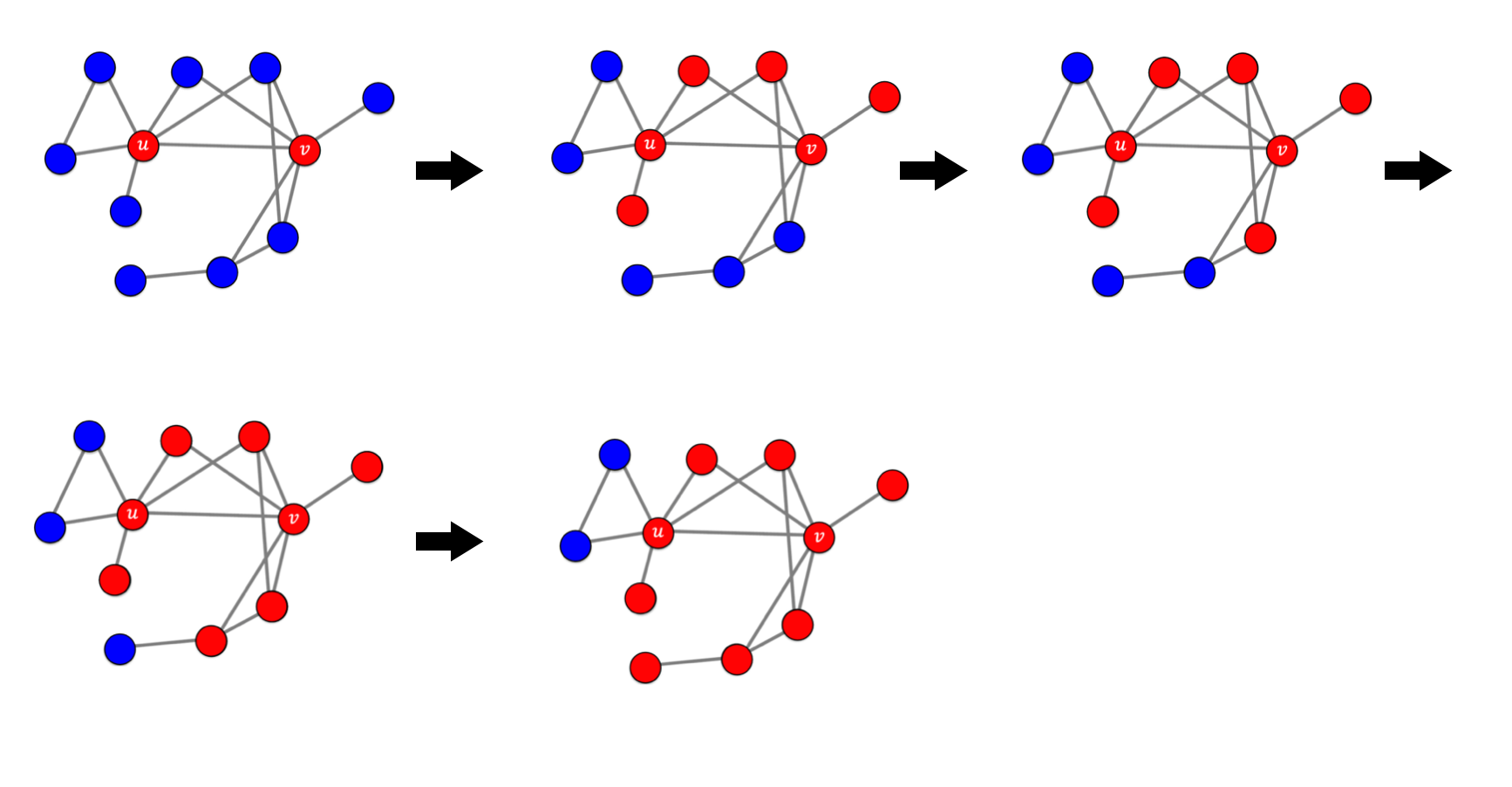
- 본 모델에는 새로운 기술(A라 칭함)을 사용하는 사람 2명(u,v)을 가정한다.
- 시드 집합(Seed set)이라 불리는 얼리 어답터들은 A를 고수한다.
- 임계치는 55%로 설정하였다.
결론
- A와의 연결이 우세하다는 결론이 나는 정점은 모두 A로 바뀌었다.
확률적 전파 모형 (Independent Cascade Model)
- 언제 사용하는가?
코로나의 전파 과정을 생각해보자. 그 누가 코로나에 걸리고 싶어 걸리는가? 이런 상황에는 ‘확률적’ 전파가 되기 때문에 확률적 전파 모형을 사용한다.
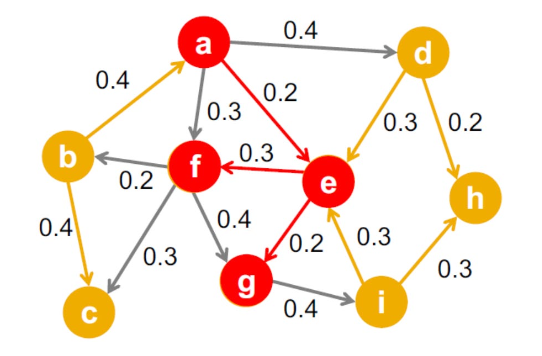
- 각 간선 (u,v) 의 가중치는 u가 감염되고 v가 감염되지 않았을 때, v가 감염될 확률을 의미한다.
- 당연하겠지만, 각각의 감염 확률은 독립적으로 작용한다.
전파모형의 진행 순서는 다음과 같다.
- 최초 감염된 노드를 시드 집합(Seed Set)이라 한다.
- 최초 감염자는 주변 노드에게 $p$확률로 병을 전파한다.
- 위 과정을 반복한다.
- 새로운 감염자가 나타나지 않는다면 종료한다.
참고할 점
- 감염자는 계속 감염상태로 남아있음에 유의하자.
- 감염자의 회복을 고려하는 경우, SIS, SIR 등의 다른 전파 모형들이 있다.
전파 최대화 문제 (Influence Maximization) 바이럴 마케팅
- 바이럴 마케팅의 경우 효과적이기 위해서는 시작점이 굉장히 중요하다 (시작점에 따라 전파속도, 범위가 차이나기 때문)
- 때문에 어떠한 시드집합을 고르냐가 가장 중요한 관건이다.
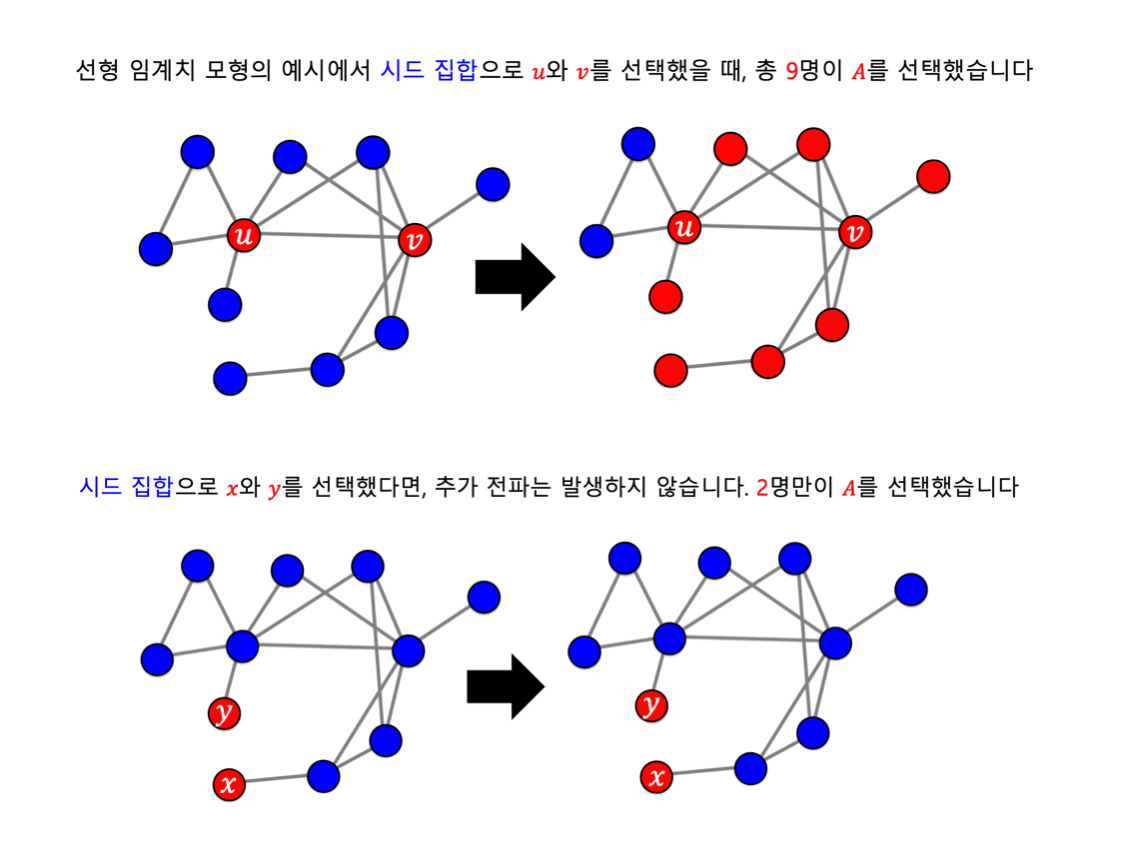
이러한 경우 때문에, 전파를 최대화 하는 시드 집합을 찾는 !!!문제!!! 를 전파 최대화(Influence Maximization) 문제라 일컫는다.
정점 중심적 휴리스틱

- 전파 최대화 문제는 굉장히 어려운 문제임이 이미 증명되었다.
- 때문에 까불지말고 휴리스틱 방법을 이용하자.
휴리스틱 : 실험적으로는 잘 동작할 수 있지만, 이론적으로는 정확도에 대해서 어떠한 보장도 할 수 없음
- 즉, 시드 집합의 크기가 k개로 고정되어 있을 때, 정점의 중심성이 높은 순으로 k개 정점 선택하는 방법이다
- 정점의 중심성을 측정하는 방법에는 페이지랭크 점수, 연결 중심성, 근접 중심성, 매개 중심성 등이 있다
- 합리적인 방법이지만, 최고의 시드 집합을 찾는다는 보장은 없다
탐욕 알고리즘
- 탐욕 알고리즘은 시드 집합의 원소, 즉 최초 전파자를 한번에 한 명씩 선택 한다
- 즉, 정점의 집합을 {1, 2, … , ∣V∣}라고 할 경우 구체적인 단계는 다음과 같다 집합 {1},{2}, … ,{∣V∣}를 비교하여, 전파를 최대화하는 시드 집합을 찾는다
- 이 때, 전파의 크기를 비교하기 위해 시뮬레이션을 반복하여 평균 값을 사용한다 뽑힌 집합을 {x} 라고 하자
- 집합 {x, 1},{x, 2}, … ,{x, ∣V∣}를 비교하여, 전파를 최대화하는 시드 집합을 찾는다 뽑힌 집합을 {x,y} 라고 하자 = 집합 {x,y, 1},{x,y, 2}, … ,{x,y, ∣V∣}를 비교하여, 전파를 최대화하는 시드 집합을 찾는다
- 뽑힌 집합을 {x,y,z} 라고 하자
- 위 과정을 목표하는 크기의 시드 집합에 도달할 때까지 반복 한다
즉, 탐욕 알고리즘은 최초 전파자 간의 조합의 효과를 고려하지 않고 근시안적으로 최초 전파자를 선택하는 과정을 반복한다
- 탐욕 알고리즘은 얼마나 정확한가?
- 독립 전파 모형에 탐욕 알고리즘을 사용할 경우, 이론적으로 정확도가 일부 보장된다
- 항상, 즉 입력 그래프와 무관하게 다음 부등식이 성립한다
- 탐욕 알고리즘으로 찾은 시드 집합의 의한 전파의 (평균) 크기 $≥ (1− e1)×$ 최고의 시드 집합에 의한 전파의(평균) 크기 $≈0.632×$ 최고의 시드 집합에 의한 전파의 (평균) 크기
- 즉, 탐욕 알고리즘으로 시드 집합의 평균 전파 크기가 최고의 시드 집합에 의한 평균 전파 크기보다 적어도 0.632배 된다는것이 수학적으로 증명되있다
- 다시 말해, 탐욕 알고리즘의 최저 성능은 수학적으로 보장되어 있다
