실제 그래프의 구조적 효과
- 작은 세상 효과
- 연결성의 두터운-꼬리 분포
- 거대 연결 요소
- 군집 구조
실제그래프 vs 랜덤 그래프
- 실제그래프(Real Graph): 다양한 복잡계로 부터 얻어진 그래프
- 예시: 소셜 네트워크, 전자상거래 구매 내역, 인터넷, 웹, 뇌, 단백질 상호작용, 지식 그래프 등
- (정점: 사용자, 간선: 주고받은 메시지)로 정의할 수 있다.
- 랜덤 그래프(Random Graph): 확률적 과정을 통해 생성한 그래프
- 여기서는 가장 기초적인, 에르되스-레니 랜덤 그래프(Erdős-Rényi Random Graph) 사용
[랜덤 그래프] 에르뇌스-레니 랜덤그래프 $G(n,p)$
- 정의: 임의의 두 정점 사이에 간선이 존재하는지 여부는 동일한 확률 분포에 의해 결정된다.
- 𝑛개의 정점을 가진다.
- 임의의 두 개의 정점 사이에 간선이 존재할 확률은 𝑝 이다.
- 정점 간의 연결은 서로 독립적(Independent)이다.
Q. $G(3,0.3)$ 에 의해 생성 될 수 있는 각각의 확률은?
출처 : ganta.log
작은 세상 효과(Small-world Effect)
- 필수 개념: 경로, 거리 및 지름
- 실제 그래프의 두 정점 사이의 거리는 작다.
- 적은 단계만 거치면, 많은 사람들과 연결될 수 있음을 의미한다.
- 실험: 여섯 단계 분리(Six Degrees of Separataion) 실험
- 속담: “사돈의 팔촌” - 아무리 먼 관계도 결국은 사돈의 팔촌(10촌 관계)
랜덤 그래프에서의 작은 세상 효과?
작은 세상 효과는 높은 확률로 랜덤 그래프에도 존재한다.
모든 사람이 100명의 지인이 있다고 가정해보면,
다섯 단계를 거치면 최대 100억(= 1005)명의 사람과 연결될 수 있다.
단, 실제로는 지인의 중복 때문에 100억 명보다는 적은 사람일 겁니다 하지만 여전히 많은 사람과 연결될 가능성이 높다.
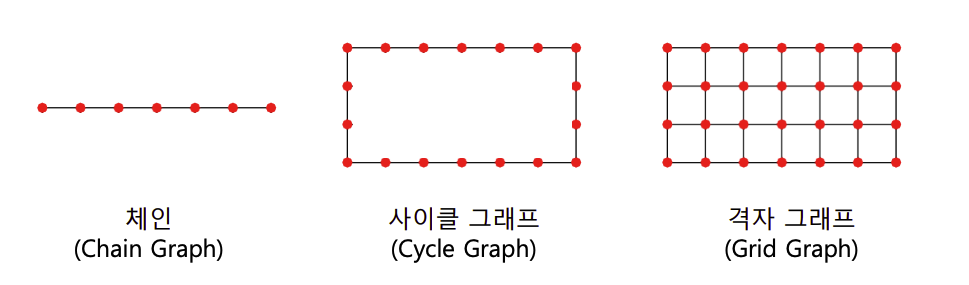
체인(Chain), 사이클(Cycle), 격자(Grid) 그래프에서는 작은 세상 효과가 존재하지 않는다.
- 경로(path)
- 정점 u와 v의 사이의 경로(path)는 다음과 같은 조건을 만족하는 정점들의 순열(Sequence)이다.
- ✔️ u에서 시작해서 v에서 끝나야 한다.
- ✔️ 순열에서 연속된 정점은 간선으로 연결되어 있어야 한다.
- 길이
- 경로의 길이는 해당 경로 상에 놓이는 간선의 수로 정의
- 거리(Distance)
- 정점 u와 v의 사이의 거리(Distance)는 u와 v사이의 최단 경로의 길이이다.
- 지름(Diameter)
- 그래프의 지름(Diameter)은 정점 쌍의 거리 간 최댓값이다.
출처 : ganta.log
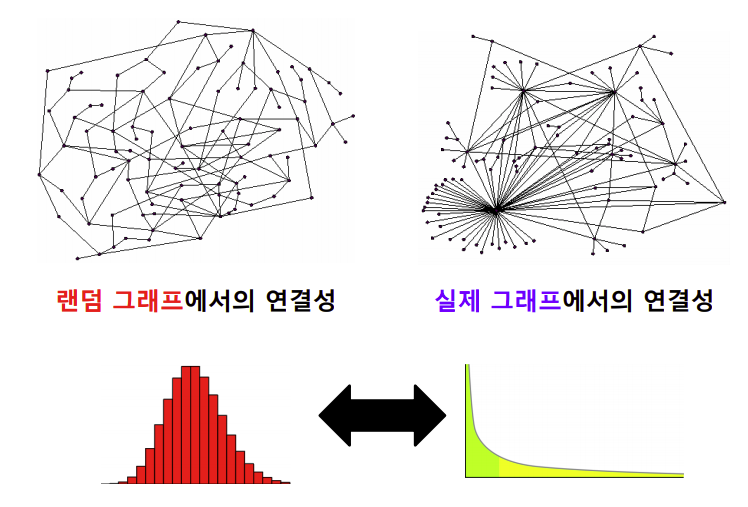
연결성의 두터운 꼬리 분포 vs 랜덤 분포
 출처 : ganta.log
출처 : ganta.log
- 필수 개념 : 연결성
- 실제 그래프의 연결성 분포는 두터운 꼬리(heavy tail)을 가진다.
- 즉, 연결성이 매우 높은 허브 정점이 존재함을 의미한다.
- 연결성이 낮은 정점은 많으나, 연결성이 큰 노드의 수는 적다.
랜덤 그래프는 높은 확률로 정규분포와 유사하다. 연결성이 매우 높은 허브(hub)가 존재할 확률은 0에 가깝다. 정규 분포와 유사한 예시로는 키의 분포가 있다. 키가 10미터를 넘는 극단적 예시는 존재하지 않는다.
거대 연결 요소 (Giant Connected Component)
- 필수 개념 : 연결 요소
- 거대 연결 요소는 대다수의 정점을 포함한다.
- 실제 그래프에서는 대다수의 정점을 포함하는 거대 연결 요소, 거대 그룹이 존재함.
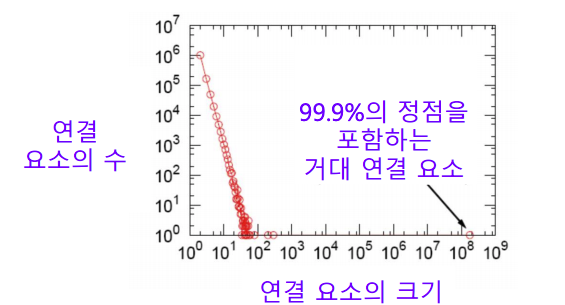
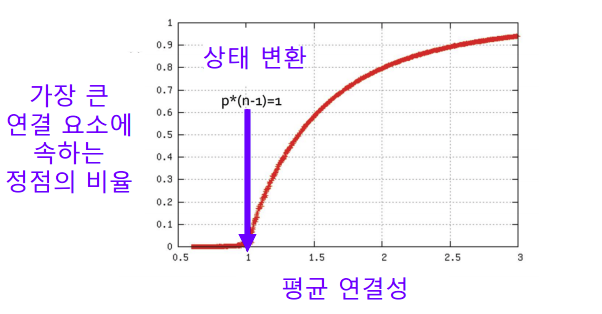
- 랜덤 그래프는 높은 확률로 거대 연결 요소(Giant Connected Component)가 존재한다. 이때, 정점들의 평균 연결성이 1 보다 충분히 커야 한다.(p∗(n−1)=1) 직관적으로 생각 해 보면 간선이 하나 있어야 연결요소가 생기는데 p∗(n−1)은 (n−1)을 간선의 수로 본다면 간선이 생기는 수로 써 볼 수 있다. 따라서, 이 값이 1이 넘어야 급격하게 연결 요소가 생긴다고 생각 할 수 있다.
군집 구조
군집
군집이란 다음 조건들을 만족하는 정점들의 집합.
- 집합에 속하는 정점 사이에는 많은 간선이 존재.
- 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재.
지역적 군집 계수
지역적 군집 계수(Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 측정한다. 정점 $i$ 의 지역적 군집 계수는 정점 i의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 말한다. 정점 $i$ 의 지역적 군집 계수를 $C_i$ 로 표현 할 시 예시는 다음과 같다.
예시)

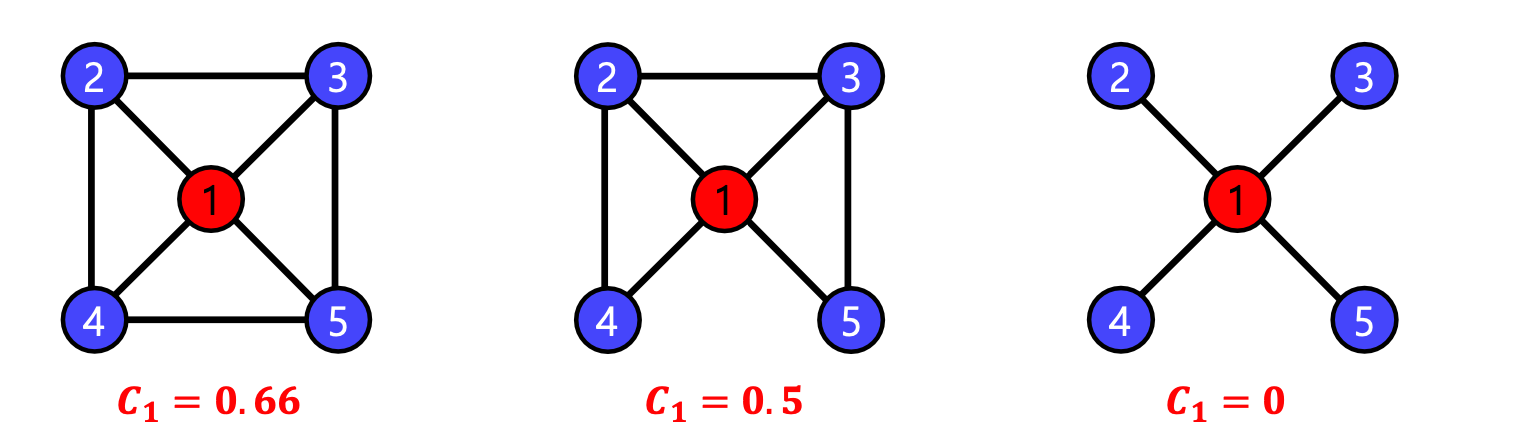
Q.지역적 군집 계수가 군집이랑 어떻게 연결되는가?
정점 𝑖의 지역적 군집 계수가 매우 높다고 하자.
즉, 정점 𝑖의 이웃들도 높은 확률로 서로 간선으로 연결되어 있다.
정점 𝑖와 그 이웃들은 높은 확률로 군집을 형성한다.
전역 군집 계수
- 전체 그래프에서 군집의 형성 정도를 측정
- 그래프 $G$의 전역 군집 계수는 각 정점에서 지역적 군집 계수의 평균이다.
- 단, 지역적 군집 계수가 정의되지 않는 정점은 제외한다.
출처 : ganta.log
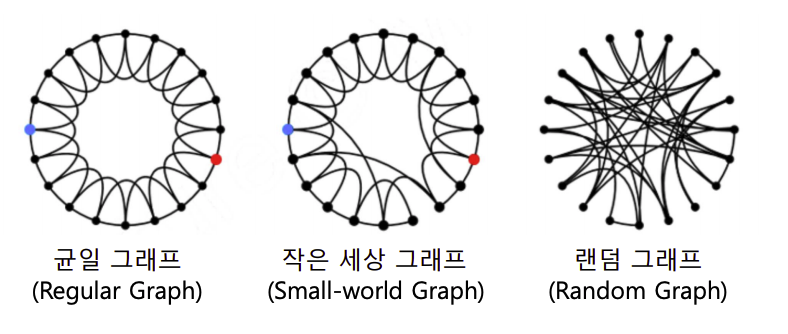
균일 그래프 : 군집계수 - 크다, 지름 - 크다
작은 세상 그래프 : 군집계수 - 크다, 지름 - 작다
랜덤 그래프 : 군집계수 - 작다, 지름 - 작다

