Convolutional Neural Networks (CNN)
대표적 CNN 모델들에 대해 알아본다. (매 대회에서 1등했던 모델들)
- AlexNet
- 최초로 Deep Learning을 이용하여 ILSVRC에서 수상
- VGGNet
- 3x3 Convolution을 이용하여 Receptive field는 유지하면서 더 깊은 네트워크를 구성
- GoogLeNet
- Inception blocks 을 제안
- ResNet
- Residual connection(Skip connection)이라는 구조를 제안
- DenseNet
- Resnet과 비슷한 아이디어지만 Addition이 아닌 Concatenation을 적용한 CNN
AlexNet
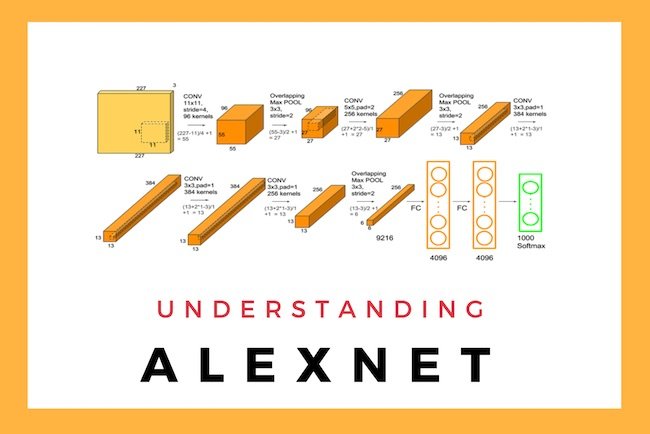
- 네트워크가 두개로 구성
- 이유: 당시 GPU 부족 ➡ 네트워크에 최대한 많은 파라미터를 넣고자
- input: 11 x 11 ➡ 그렇게 좋은 선택은 아님
- receptive field 하나의 convolutional kernel이 볼 수 있는 이미지 레벨 영역은 커짐
- 그러나 상대적으로 더 많은 파라미터 필요
- 총 depth: 8단
- Key Ideas
- Rectified Linear Unit(ReLU) Activation
- GPU implementation(2GPUs)
- Data Augmentation
- Dropout: 뉴런 중에서 몇개를 0으로 만듦
- Local response normalization
- Overlapping pooling
초록색 : 현재에 많이 사용하는 기법들.
Relu
- ReLu는 Rectified Linear Unit의 약자로 해석해보면 정류한 선형 유닛이라고 해석할 수 있다.
- ReLu를 Activation function이 발표된지는 오래되었다.
그러나 현재처럼 Neural Network에서 주된 activation function으로 사용된지는 오래되지 않았다.
Neural Network를 처음배울 때 activation function으로 sigmoid function을 사용한다. sigmoid function이 연속이여서 미분가능한점과 0과 1사이의 값을 가진다는 점 그리고 0에서 1로 변하는 점이 가파르기 때문에 사용해왔다. 그러나 기존에 사용하던 Simgoid fucntion을 ReLu가 대체하게 된 이유 중 가장 큰 것이 Gradient Vanishing 문제이다. Simgoid function은 0에서 1사이의 값을 가지는데 gradient descent를 사용해 Backpropagation 수행시 layer를 지나면서 gradient를 계속 곱하므로 gradient는 0으로 수렴하게 된다. 따라서 layer가 많아지면 잘 작동하지 않게 된다.
따라서 이러한 문제를 해결하기위해 ReLu를 새로운 activation function을 사용한다. ReLu는 입력값이 0보다 작으면 0이고 0보다 크면 입력값 그대로를 내보낸다.
출처: https://mongxmongx2.tistory.com/25 [몽이몽이몽몽이의 블로그]
VGGNet

- Increasing depth with 3 x 3 convolution filters (with stride 1)
- 3 x 3 convolution filters ➡ 이것만 사용!
- 1 x 1 convolution for fully connected layers
- 채널을 줄이기 위해서 사용된 것이 아니므로, 별로 중요하지는 않음
- Dropout (p=0.5)
- VGG16, VGG19
3x3 의 convolution filters 만 사용하였다
필터의 사이즈가 3x3 으로 고정된 이유 ? -> 발표한 논문에 의하면 연산하여 발생하는 파라미터 수가 줄어들고 ReLU 가 활성화 함수로 들어갈 수 있는 곳이 많아진다는 장점이 존재한다.
- 파라미터의 수가 차이나는 이유는?
3 x 3 x 2 = 18<5 x 5 = 25즉 필터를 작게 쓸 경우 레이어를 두개 두더라도 파라미터 수가 더 작은 효과를 볼 수 있음.
Google Net

구글넷은 22개의 층으로 구성되어 있다. 이젠 구글넷의 특징을 알아보자.
1. 1x1 컨볼루션
구조도를 보면 알겠지만, 곳곳에 1x1 컨볼루션이 존재함을 알 수 있다.
1x1 컨볼루션이 가지는 의미는 무엇일까? -> 특성맵의 갯수를 줄이는 목적으로 사용된다. 특정맵의 갯수가 줄어들면 그만큼 연산량이 줄어든다.
예를 들어, 480장의 14 x 14 사이즈의 특성맵(14 x 14 x 480)이 있다고 가정해보자. 이것을 48개의 5 x 5 x 480의 필터커널로 컨볼루션을 해주면 48장의 14 x 14의 특성맵(14 x 14 x 48)이 생성된다. (zero padding을 2로, 컨볼루션 보폭은 1로 설정했다고 가정했다.) 이때 필요한 연산횟수는 얼마나 될까? 바로 (14 x 14 x 48) x (5 x 5 x 480) = 약 112.9M이 된다.
이번에는 480장의 14 x 14 특성맵(14 x 14 x 480)을 먼저 16개의 1 x 1 x 480의 필터커널로 컨볼루션을 해줘 특성맵의 갯수를 줄여보자. 결과적으로 16장의 14 x 14의 특성맵(14 x 14 x 16)이 생성된다. 480장의 특성맵이 16장의 특성맵으로 줄어든 것에 주목하자. 이 14 x 14 x 16 특성맵을 48개의 5 x 5 x 16의 필터커널로 컨볼루션을 해주면 48장의 14 x 14의 특성맵(14 x 14 x 48)이 생성된다. 위에서 1 x 1 컨볼루션이 없을 때와 결과적으로 산출된 특성맵의 크기와 깊이는 같다는 것을 확인하자. 그럼 이때 필요한 연산횟수는 얼마일까? (14 x 14 x 16)(1 x 1 x 480) + (14 x 14 x 48)(5 x 5 x 16) = 약 5.3M이다. 112.9M에 비해 훨씬 더 적은 연산량을 가짐을 확인할 수 있다. 연산량을 줄일 수 있다는 점은 네트워크를 더 깊이 만들수 있게 도와준다는 점에서 중요하다.

2. Inception module
이번에는 GoogleNet 의 핵심인 Inception 모듈에 대해 알아보자.
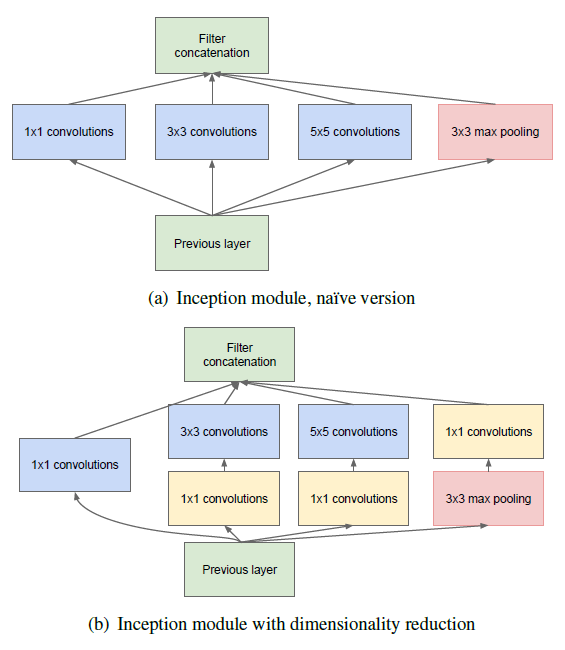
GoogleNet은 이전 층에서 생성된 특성맵을 1x1, 3x3, 5x5, 3x3 max pooling 의 결과로 얻은 특성맵들을 하나로 합쳐주며 쌓아준다. 이 결과는 좀 더 다양한 종류의 특성이 도출되는 효과를 가진다. 여기에 1x1 컨볼루션과 함께해 당연히 연산량은 더더욱 줄어든다.
ResNet
ResNet은 residual repesentation 함수를 학습함으로써 신경망이 152 layer까지 가질 수 있다. ResNet은 이전 layer의 입력을 다음 layer로 전달하기 위해 skip connection(또는 shorcut connection)을 사용한다. 이 skip connection은 깊은 신경망이 가능하게 하고 ResNet은 ILSVRC 2015 우승을 했다.
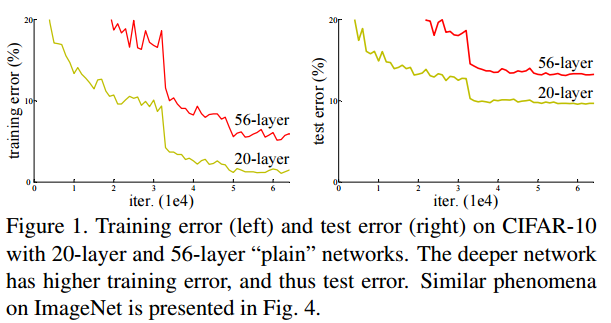
보통의 경우 신경망이 깊어질 경우 더 정확한 예측을 할거라고 예상하지만, 신경망이 깊을 때, 작은 미분값이 여러번 곱해지면 0에 가까워 지고 큰 미분값이 여러번 곱해지면 값이 매우 커지게 된다. 즉 기울기 소실, 기울기 폭발 현상이 일어날 수 있다.
Skip / Shortcut Connection in Residual Network (ResNet)
- 따라서 위와 같은 문제를 해결하기 위하여 입력 x의 값을 몇번의 layer 이후에 출력값에 더해주는 skit/shortcut connection 이 나오게 된다.
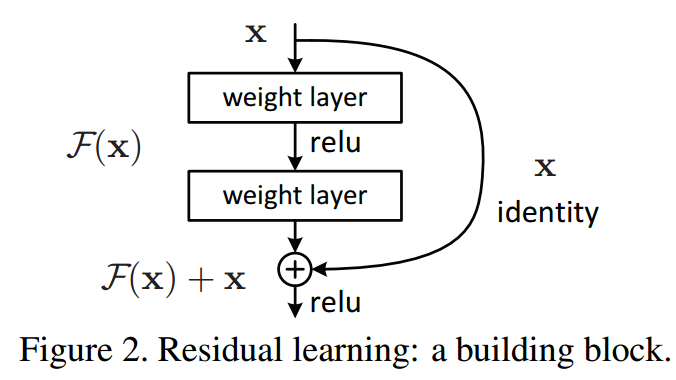
기존의 신경망은 H(x) = x가 되도록 학습 했다. skip connection에 의해 출력값에 x를 더하고 H(x) = F(x) + x로 정의한다. 그리고 F(x) = 0이 되도록 학습하여 H(x) = 0 + x가 되도록 한다. 이 방법이 최적화하기 훨씬 쉽다고 한다. 미분을 했을 때 더해진 x가 1이 되어 기울기 소실 문제가 해결된다.
기울기 소실 문제가 해결되면 정확도가 감소되지 않고 신경망의 layer를 깊게 쌓을 수 있어 더 나은 성능의 신경망을 구축할 수 있다!.
DenseNet
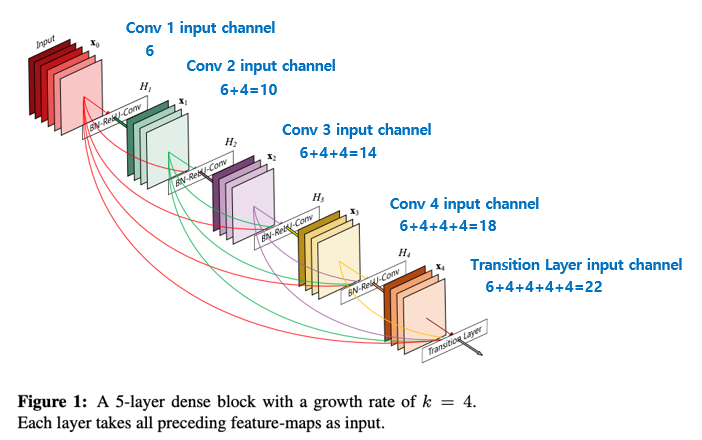
Dense Connectivity
DenseNet 은 모든 레이어의 피쳐맵을 연결한다. 이전 레이어의 피쳐맵을 그 이후의 모든 레이어에 연결한다.
하지만 여기서 차이점이 있다. ResNet과 달리 연결할때, 덧셈이 아닌 concatenate(사슬처럼 잇다)를 수행한다. 때문에 연결할 때, 피쳐맵의 크기가 동일해야한다는 점도 작용한다.
- 이로인해 얻는 장점은?
- Strong gradient flow, information flow : 기존의 CNN 모델은 많은 레이어를 통과할 경우, 처음 레이어의 피쳐맵에 대한 정보가 끝에 다다라서 사라지지만 DensNet의 경우 정보가 소실되지 않는다.
- 파라미터수와 연산량이 적다 : DenseNet은 적은 채널수를 이용하기 때문에, 적은 채널 수의 피쳐맵을 생성한다. 그리고 이 피쳐맵이 이전 레이어의 피쳐맵과 결합하여 다음 레이어에 전달된다.
Dense Block
Concatenation 을 수행하기 위해서는, 피채맵의 크기가 동일해야 하지만, 피쳐맵의 크기를 감소시키는 Pooling 연산 또한 CNN에서 필수적인 요소이다.
따라서 이를 해결하기 위해, Dense Block 을 수행한다.

- transition layer ( 그림상에서 convolution , pooling )
- 피쳐맵의 크기와 채널을 줄인다.
- 차원 축소의 개념.
- Dense Block
- 피쳐맵의 크기와 채널이 늘어난다.
- 채널의 수가 기하급수적으로 증가한다.


